Sir Roger Penrose, nhà toán học vừa đoạt giải Nobel Vật Lý năm nay, là một nhà bác học theo đúng nghĩa xưa của chữ đó. Tôi đã nói về giải Nobel của ông trong kỳ trước, kỳ này tôi nói thêm về ông và về lý do tôi nghĩ lẽ ra ông đã phải được Nobel Hóa Học nữa.
Không chỉ là một nhà khoa học, Penrose còn suy nghĩ và viết về Triết. Ông phát triển một lý thuyết về ý thức của người (hay của con vật) và cho rằng ý thức cao hơn các hiện tượng tự nhiên và các ý thuyết Vật Lý không đủ để giải thích ý thức.
Ý thức, trong triết, miêu tả sự nhận biết về thế giới chung quanh. Thí dụ, một con chó thấy cái cây đổ về hướng nó thì nó ý thức được nó sắp bị đè bẹp và chạy đi chỗ khác. Con chó hiểu điều này dù có thể từ trước đến nay nó chưa thấy cái cây đổ bao giờ.
Lý thuyết này cho rằng nếu con người (hay con vật) nhìn thấy A (cái cây đổ) và kết luật được B (cây sắp đè mình chết), thì phải có một con đường nào đó dẫn từ A tới B. Con đường đó phải là một thuật toán (algorithm). Tức là phản ứng của con chó có thể viết thành một algorithm, thí dụ như:
Nếu (một vật đang chuyển động) và (nó chuyển động về hướng mình) thì (tránh ra chỗ khác)
Con chó làm điều này được thì computer làm được. Chỉ là algorithm mà! Algorithm là nghề của computer!
Nhưng Penrose suy luận ngược lại. Ông cho rằng có những thứ đi được từ A đến B nhưng không viết được thành algorithm. Ngay trong ngành computer người ta cũng biết điều này. Có những quy trình trong computer có câu trả lời nhất định nhưng không xác định được bằng algorithm nào cả. Ông cho rằng ý thức của con người hay con vật có ý nghĩa cao hơn chữ không chỉ là những thuật toán.
Trên báo Rice Thresher của đại học Rice ở Texas, Giáo sư Toán hưu trí Raymond Wells kể về lần Penrose đến nói chuyện về ý thức.
“Khi ông tới diễn thuyết trong một loạt bài giảng dựa trên những chương chính của quyển sách ông viết về ý thức, gần như toàn bộ đại học Rice đều đến nghe, từ Viện trưởng, Provost (viện phó học vụ), các khoa trưởng, cũng như nhiều giáo sư và sinh viên. Tất cả chúng tôi đều có cảm tưởng đang đứng trước một cái gì rất đặc biệt.”
Nhưng Triết là nghề của người khác. Để tôi quay lại Toán.
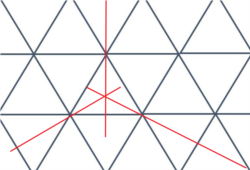
Đây là hình mặt tiền của toà nhà khoa Vật Lý đại học Rice. Trên tường toà nhà có hoa văn gồm các hình tứ giác xếp lại.
Nếu nhìn kỹ, sẽ thấy toàn bộ mặt tường chỉ có hai mẫu hình tứ giác, một hình như mũi tên và một hình như cánh diều.
Cách sắp xếp này do Penrose sáng chế ra và mang tên Penrose Tiling.
Trong hình học, ngành nghiên cứu về việc sắp xếp các hình lập lại để lát đầy một mặt phẳng được gọi là “tessellation.” Tôi đã có dịp nói về tessellation trong một bài trước. “Sắp xếp các hình lập lại để lát đầy một mặt phẳng” nghe có vẻ khoa học ra phết, nhưng thực ra thì như ông thợ hồ lát gạch thôi, nên tessellation còn gọi nôm na là tiling.
Thế thì nếu mình lát gạch sàn nhà, dùng hình tam giác đều 3 cạnh và đối xứng xoay theo 1/3 vòng tròn thì rất dễ.
Dùng hình tứ giác đều tức hình vuông 4 cạnh và đối xứng xoay theo 1/4 vòng tròn, cũng như hình lục giác đều t cạnh và đối xứng xoay theo 1/6 vòng tròn như hình tổ ong, cũng dễ luôn. Không những đối xứng theo góc, những hình này còn lập lại theo đường thẳng.
Số 3, 4, 6 đều dễ, nhưng còn số 5 ở giữa thì sao? Ghép hình ngũ giác có lát được sàn đối xứng xoay theo 1/5 vòng tròn được không? Hình ngũ giác đều ghép lại thì không lát được sàn nhà vì bị hở một miếng. Chành ra ba góc da còn thiếu là vậy.
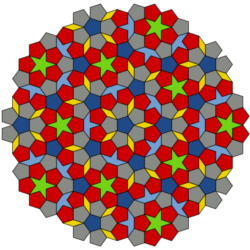
Không ai biết cách xếp gạch cho đối xứng xoay theo 1/5 vòng tròn -- cho tới khi có Roger Penrose. Năm 1974, ông chứng minh được rằng có rất nhiều cách để xếp gạch để lát hết mặt phẳng với đối xứng xoay theo 1/5 vòng tròn.
Phiên bản đầu tiên do Penrose làm ra có 6 mẫu gạch lập lại, hình ngũ giác, hình ngôi sao 5 cánh, hình thuyền buồm (3 cánh sao), và hình thoi. Sau này ông rút số mẫu gạch chỉ cần 2 mẫu hình thoi, hoặc 2 mẫu, một hình mũi tên một hình cánh diều.
Hình chụp Penrose trên đầu bài là ở sảnh toà nhà Mitchell Institute, đại học Texas A&M. Gạch lát sàn nhà gồm 2 mẫu hình thoi ghép lại và có đối xứng xoay theo hình ngũ giác, 1/5 vòng tròn.
Trước Penrose, không ai biết là điều này có thể làm được. Sau Penrose, người ta biết nó có thể làm được. Và qua đó người ta bắt đầu đi tìm nó trong thiên nhiên và quả nhiên người ta phát hiện ra là có sự lát gạch với đối xứng xoay theo 1/5 vòng tròn trong thiên nhiên.
Và đó là điều Dan Shechtman, đại học Technion - Israel Institute of Technology ở Israel đã làm. Năm 1982, khi nghỉ sabattical ở Technion để làm việc 2 năm tại National Institute of Standards and Technology ở Mỹ (Viện Tiêu chuẩn và Kỹ thuật Quốc gia), ông phát hiện ra một cấu trúc nguyên tử lạ lùng, là nó đối xứng xoay vòng nhưng không lập lại theo đường thẳng.
Nói cách khác, các nguyên tử này sắp xếp theo Penrose Tiling trên mặt cầu.
Thí nghiệm của Schechtman là ông lấy hỗn hợp nhôm manganese, làm lạnh nó thiệt nhanh để nó đừng biến thành tinh thể (crystal). Rồi ông bắn điện tử vào đó cho điện tử báng văng ra ngoài rồi chụp hình điện tử đó. Dùng hình chụp điện tử ông sẽ thấy cấu trúc của hỗn hợp này, một phương pháp gọi là diffraction.
Thế thì Schechtman biết là có thể có đối xứng 1/3 vòng tròn, 1/4 vòng tròn, hay 1/6 vòng tròn. Lúc đó ông chưa biết về công trình của Penrose nên không biết là có thể có đối xứng 1/5 vòng tròn.
Nhưng khi chụp hình thì ông thấy rành rành có đối xứng vòng tròn 10 nguyên tử.
Thế là thế nào?
Trong hoá học, khi nguyên tử sắp xếp ngay hàng thẳng lối lập lại thì gọi là tinh thể. Schechtman thấy nguyên tử trong hỗn hợp này sắp xếp cũng hơi hơi ngay hàng thẳng lối theo vòng tròn nhưng không lập lại theo đường thẳng. Ông gọi nó là quasicrystal, gần như tinh thể.
Dùng phương pháp của Penrose, hai nhà vật lý học Dov Levine và Paul Steinhardt tiên đoán có thể có cấu trúc nguyên tử theo Penrose Tiling, 10 nguyên tử sắp xếp đối xứng xoay theo 1/5 vòng tròn. Đây chính là điều Schechtman tìm ra. Trong sổ tay của Schechtman còn ghi lại sự ngạc nhiên của ông khi phát hiện quasicrystal: “10 lần???” với 3 dấu chấm hỏi.
Đây là một khám phá quan trọng, nhưng xui cho Schechtman, Linus Pauling không nghĩ vậy.
Pauling là ai? Trên thế giới chỉ có 4 người từng đoạt 2 giải Nobel, và Pauling (1901–1994) là một. Chỉ có 2 người đoạt giải Nobel trong hai ngành khác nhau, là Marie Curie và Pauling. Và Pauling là người duy nhất đoạt 2 giải Nobel, Hoá Học và Hoà Bình, mà không chia chung với ai hết.
Nói tóm lại, Linus Pauling là trùm ngành Hóa.
Pauling nhất quyết không chấp nhận khái niệm quasicrystal. Đối với ông, nếu nguyên tử không kết thành tinh thể là nó chưa kết thành gì cả. “Không có cái gọi là gần-như-tinh thể,” Pauling quả quyết, “chỉ có người gần-như-khoa học gia.” Cả thế giới Hoá học hùa theo chống Schechtman. Ngay sếp của Schechtman cũng yêu cầu ông qua làm việc ở nhóm nghiên cứu khác cho khuất mắt.
“Trong một thời gian dài chỉ có mình tôi chống lại thế giới,” Schechtman kể. “Tôi bị chế riễu, bị liên tục nghe giảng những bài căn bản về lý thuyết tinh thể. Cầm đầu phe chống đối là Linus Pauling... (Nhưng) ông đã sai, và sau một thời gian tôi lại thích trận đánh khoa học này, biết rằng ông ấy sai.”
Pauling đã sai vì không nhận ra tầm quan trọng của Penrose Tiling. Penrose Tiling là nền tảng toán học cho ngành nghiên cứu quasicrystal, và qua việc khám phá ra quasicrystal, Schechtman cuối cùng thuyết phục được cộng đồng Hóa học. Năm 2011 Schechtman đoạt giải Nobel. Ủy ban Nobel Hóa Học đã không chia một phần giải này cho Penrose, nhưng nếu có thì cũng xứng đáng lắm.