Ở Việt Nam học sinh phổ thông phải học lượng giác nên có lẽ nhiều người còn nhớ có cái gọi là “sin,” “cos” và “tang.” Tiếng Anh gọi là “sine,” “cosine,” và “tangent.” Hàm tang ở Việt Nam có thời viết tắt là tg, bây giờ viết tắt là tan, giống ở Mỹ.
Người Mỹ tiếng là kém toán, chương trình phổ thông ở Mỹ không bắt buộc học lượng giác, nhưng nhiều người vẫn biết hàm sin, vì hầu như ai cũng biết cái đồ thị lên xuống nhấp nhô và nó mang tên gọi “sine wave” - sóng sin. Cosine với tangent thì chắc không biết chứ sine thì chắc chắn biết.
Trong một tam giác vuông, sin của một góc nhọn được định nghĩa là cạnh đối chia cho cạnh huyền của tam giác. Cạnh huyền là cạnh dài nhất trong tam giác vuông, tiếng Anh gọi là hypotenuse.
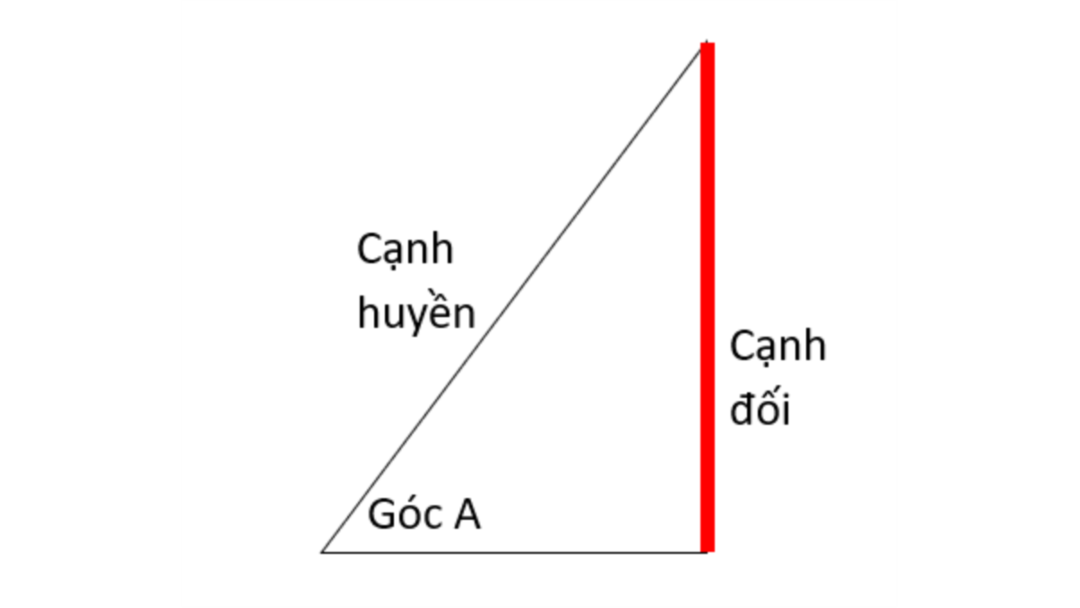
Cạnh huyền là cạnh dài nhất trong tam giác vuông, tiếng Anh gọi là hypotenuse.
Để dễ nhớ, công thức này (cùng với công thức cho cos và tang) ở Mỹ được dạy với cụm từ “SOH CAH TOA.” SOH: Sine = Opposite / Hypotenuse; CAH: Cosine = Adjacent / Hypotenuse; TOA: Tangent = Opposite / Adjacent.
Nhưng tại sao lại gọi tên hàm sin là sin? Tại tiếng La-tinh là sinus. Nhưng tại sao tiếng La-tinh lại là sinus?
À, tin buồn cho mọi người nhá. Tên của hàm lượng giác nổi tiếng, nổi tiếng đến nỗi những người không học lượng giác cũng biết tên, lại là một lỗi lầm.
Hàm lượng giác đến với chúng ta hiện nay là qua ngả Ả rập. Sau thời hoàng kim của nền văn minh Ai Cập, Hy Lạp, La Mã, châu Âu rơi vào một thời gian dài, gần cả ngàn năm, mất hết các kiến thức khoa học cũ, chìm đắm trong chiến tranh và mê tín dị đoan. Văn chương thần thoại thì hay lắm, nhưng khoa học thì không. Các kiến thức cũ được truyền qua thế giới Ả rập, và phải tới thế kỷ 11, 12, khoa học mới về lại châu Âu do những tên tuổi như Fibonacci hay Gherardo da Cremona mang từ Ả rập về.
Hàm sin cụ thể đến từ một nhà toán học Ấn Độ thế kỷ thứ 5, Aryabhata (476-550). Ông phát minh ra hàm sin khi nghiên cứu quỹ đạo các sao và các hành tinh.
Nếu vẽ góc A ở ngay tâm vòng tròn, thì đường bán kính của hình tròn chính là cạnh huyền của tam giác. Vậy sin của góc A sẽ là cạnh đối chia cho cạnh huyền, và nếu đường bán kính = 1 thì sin A = đối chia 1, bằng đối.
Trong hình như ở dưới đây, phần bên phải nhìn giống cây cung, chỗ góc A và đường ngang nhìn giống mũi tên, và sin A là một nửa dây cung.
Phần bên phải nhìn giống cây cung, chỗ góc A và đường ngang nhìn giống mũi tên, và sin A là một nửa dây cung.
Đó là định nghĩa của sin A, theo Aryabhata. Ông gọi tên hàm này là ardha-jya, tiếng Phạn (Sanskrit) có nghĩ là “nửa dây.” Ngoài hàm sin, Aryabhata còn định nghĩa hàm kotijya tương đương với cos, và hàm utkramajiya tương đương 1 – cos.
Từ ardha-jya có nghĩa là nửa dây, nhiều người gọi tắt là jya, và khi các nhà khoa học Ả rập dịch qua tiếng Ả rập, họ phiên âm thành jiba và viết tắt là jb.
Từ Ả rập, khái niệm này được mang vào châu Âu qua Gherardo da Cremona (1114-1187). Ông dịch lượng giác từ tiếng Ả rập qua La tinh. Ông thấy chữ jb viết tắt của jiba. Tuy nhiên, trong tiếng Ả rập chữ jiba không có nghĩa gì cả -- họ chỉ dùng jiba để phiên âm “jya” của tiếng Phạn. Gherardo thấy chữ tắt jb thì tưởng là jaib, có nghĩa là cái hốc (núi) hay cái vũng (nước).
Nên ông dịch ra tiếng La tinh là sinus , cũng có nghĩa là cái hốc. Chả liên quan gì tới nghĩa gốc là dây cung. Và từ đó ta có hàm sin.
Nói dông dài thì tóm gọn lại, lý do hàm đó gọi là sin là vì lỗi của cậu đánh máy.


