Có người đề nghị tôi viết về hai thành tựu nổi tiếng của hai nhà toán học Việt Nam, bổ đề cơ bản do GS Ngô Bảo Châu chứng minh, và lát cắt Tụy của GS Hoàng Tụy.
Bổ đề cơ bản không thuộc ngành của tôi. Để từ từ tôi cầu cứu đồng nghiệp. Hoặc trong số độc giả có ai rành bổ đề này giúp tôi với.
Lát cắt Tụy thuộc ngành operations research (GS Tụy dịch là ngành “vận trù học”) thì tôi có học, nên sẽ cố gắng giải thích ở dưới, có gì sai xin sửa dùm.
GS Hoàng Tụy (1927-2019), người tỉnh Quảng Nam, là chủ nhiệm khoa Toán Đại học Tổng hợp Hà Nội và là Viện trưởng Viện Toán học Việt Nam từ năm 1980 đến 1989. Ông tốt nghiệp tiến sĩ toán đại học Lomonosov (Moscow State University), Liên Xô. Ông nội ông là em ruột Tổng đốc Hoàng Diệu, người tuẫn tiết khi quân Pháp chiếm thành Hà Nội năm 1882.
GS Tụy còn quan tâm và đóng góp nhiều về các vấn đề giáo dục và phát triển. Năm 2007, ông 9 nhà nghiên cứu độc lập tên tuổi khác thành lập Viện Nghiên cứu Phát triển IDS mà ông là Chủ tịch Hội đồng Viện. Viện IDS tự giải thể năm 2009 sau khi Thủ tướng Việt Nam cấm các tổ chức nghiên cứu khoa học không cho họ công bố kết quả phản biện ngược với chính sách của Chính phủ.
Trong số báo đặc biệt của Journal of Global Optimization kỷ niệm sinh nhật 70 năm GS Hoàng Tụy, hai giáo sư chủ biên Hiroshi Konno và Takahito Kuno Đại học Công nghệ Tokyo gọi ông là lãnh tụ của chuyên ngành global optimization trong operations research, và là cha đẻ của các phương pháp tất định (không sử dụng ngẫu nhiên) để tìm tối ưu.
GS Tụy cũng được xem là người mang operations research vào Việt Nam, hoặc tối thiểu là vào miền Bắc Việt Nam. Operations research là gì? Ở các đại học Mỹ, ngành này có thể được dạy trong khoa Toán, khoa Quản trị Kinh doanh, khoa Điện toán (Computer Science), hay khoa Kỹ thuật Công nghiệp (Industrial Engineering) -- đủ thấy dùng được trong rất nhiều việc.
Một nhánh chính của ngành operations research là nghiên cứu các phương pháp tìm điểm tối ưu khi bị giới hạn. Nếu suy nghĩ kỹ về cụm từ “tìm điểm tối ưu khi bị giới hạn” sẽ thấy là mọi chuyện ở đời đều về tới cụm từ đó hết.
Tìm người yêu trong điều kiện vô giới hạn thì dễ. Ở đời không có chuyện đó. Phải tìm người yêu trong điều kiện có những giới hạn của trời, thần, người.
Lấy thí dụ. Nếu sản xuất càng nhiều xe hơi thì chi phí mỗi chiếc càng giảm.. Vậy làm cách nào để chi phí mỗi chiếc nhỏ nhất? Đó là chuyện tìm điểm tối ưu.
Có thể trả lời, dễ mà, Sản xuất thiệt nhiều xe hơi, cho nhà máy chạy 24/24. Nhiều xe hơi nhất thì chi phí mỗi chiếc thấp nhất. Đó là điểm tối ưu nếu không bị giới hạn.
Nhưng trên thực tế thì có những giới hạn về tiền, nguyên liệu, nhân sự. Vậy điểm tối ưu có giới hạn nằm ở đâu?
Nếu trả lời “có bao nhiêu tiền, có bao nhiêu nguyên liệu, có bao nhiêu nhân sự, cứ đổ vào đấy,” sẽ là câu trả lời sai.
Sai là vì, thí dụ có đủ tiền để sản xuất 200 xe hơi và có đủ nguyên liệu để sản xuất 300 xe hơi . Nếu đổ tối đa tiền và tối đa nguyên liệu thì sẽ bỏ phí mất nguyên liệu của 100 chiếc xe hơi. Không phải tối ưu.
Điểm tối ưu sẽ là một cái tối đa nào đó (tiền, hay nguyên liệu, hay nhân sự) mà có đủ các thứ còn lại. Thí dụ, nếu có đủ tiền để sản xuất 200 xe hơi, có đủ nguyên liệu để sản xuất 300 xe hơi, và có đủ nhân sự để sản xuất 150 xe hơi, mình sẽ bỏ vào tối đa nhân sự nhưng không tối đa tiền và không tối đa nguyên liệu. Và số xe hơi nên sản xuất, là 150.
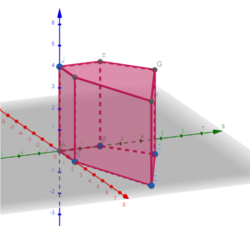
Trong operations research, những giới hạn này thường được mô hình bằng mặt phẳng trong không gian n chiều. Những mặt phẳng này tạo thành một hình khối. Và, như trong thí dụ trên, điểm tối ưu nằm ở chỗ dùng tối đa nhân sự -- nói rộng hơn, điểm tối ưu sẽ nằm trong một trong những đỉnh (góc) của hình khối đó.
Giả sử các điều kiện giới hạn có thể vẽ thành hình khối như ở trên. Điểm tối ưu (trong Toán gọi là cực trị toàn cục - global optimum) sẽ nằm ở một trong 10 đỉnh. Chỉ cần tìm ra 10 đỉnh đó ở đâu, tính xem giá trị bằng bao nhiêu, thí dụ tính chi phí xe hơi ở mỗi đỉnh là bao nhiêu. Đỉnh nào có con số thấp nhất (hay cao nhất nếu mình đang tìm con số cao nhất) đỉnh đó là chỗ tối ưu.
Rồi. Nghe thì dễ, nhưng nếu không chỉ có 10 đỉnh mà có vài trăm , vài ngàn đỉnh, thì sao?
Thí dụ như tính cách vận hành tối ưu tất cả các chuyến bay của một hãng hàng không, hay phân phối hàng trong cả một hệ thống bán lẻ, hay thiết kế mạng internet, hay sắp xếp giờ chạy của hệ thống xe buýt trong thành phố, khi một số giờ rất đông người đi và cũng rất hay bị kẹt xe và một số giờ khác thì rất vắng.
Khi hình khối có hàng trăm, hàng ngàn đỉnh, cả chuyện tìm ra toạ độ các đỉnh và chuyện tính giá trị tại các đỉnh đó đều tốn thời gian, tốn công máy tính. Cần có cách nào để không cần phải tìm ra hết các đỉnh, và cũng không nhất thiết phải check hết các đỉnh.
Có nhiều phương pháp để không phải tìm và tính giá trị tại tất cả các đỉnh. Một phương pháp thường được dạy cho sinh viên bậc cử nhân là phương pháp “simplex,” trong đó căn bản là từ một đỉnh, đi qua một đỉnh bên cạnh. Phương pháp simplex chỉ ra cách chọn hướng đi nào cho đỡ phải đi vòng qua hết các đỉnh.
Lát cắt của GS Hoàng Tụy dùng một cách hoàn toàn khác. Không tìm đường đi từ đỉnh này tới đỉnh bên cạnh, mà cắt bỏ luôn một mảng của hình khối, khỏi ngó tới luôn. Lát cắt này được GS Hoàng Tụy công bố trong một công trình nghiên cứu năm 1964 đăng trên Doklady (Proceedings) Viện Hàn lâm Khoa học Liên Xô và được dịch lại ở Mỹ trong Soviet Mathematics.
Tôi không biết chắc chắn, nhưng tôi tin rằng “Tuy cut” là lát cắt đầu tiên trong ngành operations research. , vì các nhà nghiên cứu dùng những từ như “seminal,” “path-breaking,” “landmark” để miêu tả bài của GS Tụy. Do lát cắt Tụy đòi hỏi một số điều kiện nào đó, trong đó có điều kiện “concavity,” nên “Tuy cut” còn gọi là “concavity cut.”
Một thí dụ của concavity là như ở trên, càng sản xuất nhiều xe hơi thì chi phí mỗi chiếc càng giảm. Các hàm số có kiểu “giá sỉ rẻ hơn giá lẻ” đều thỏa mãn điều kiện concavity.
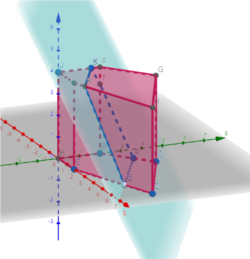
Lát cắt Tụy có thể như trong hình. Giả sử đỉnh A thoả mãn các điều kiện của một Tuy cut. Phương pháp của GS Tụy chỉ cho cách tìm một điểm A như thế, và chỉ cho cách tìm một lát cắt, thí dụ như mặt phẳng màu xanh, cắt bỏ được nguyên miếng bên trái. Không cần nhìn đến đỉnh nào phía bên đó hết. Thí dụ như trong hình này là không cần biết đến A, B, E, I, J. Bái bai không cần biết em là ai, không cần biết em ở đâu, mà vẫn biết chắc chắn em không phải điểm tối ưu. Chỉ còn lại C, D, F, G, H thôi.
Trong những đỉnh còn lại, nếu tìm được một đỉnh thoả mãn các điều kiện của một Tuy cut thì lại cắt tiếp. Phương pháp của GS Tụy cho phép tiết kiệm thời gian và công sức không chỉ một lần mà nhiều lần. Cắt và tìm và cắt và tìm cho tới khi cắt đỉnh cuối cùng thì chính hắn là điểm tối ưu.
Trong ngành operations research, lát cắt Tụy là một tiến bộ quan trọng. Trang Google Scholar đếm ra tới 335 lần bài nghiên cứu năm 1964 của GS Tụy được trích dẫn. Đó chỉ là bản ở Mỹ trong Soviet Mathematics, chưa đếm bản gốc trên Doklady ở Liên Xô. Các bài nghiên cứu sau này của GS Tụy cũng được trích dẫn mấy trăm lần, chưa kể các sách và chương sách.
Cuốn sách về tối ưu hoá của GS Tụy, Convex Analysis and Global Optimization được nhà Springer xuất bản tới lần thứ hai. Trang web của nhà xuất bản này cho thấy bản ebook của cuốn sách đã được tải về 34,000 lần. Cuốn sách ông đồng tác giả với GS Reiner Horst đại học Trier ở Đức, Global Optimization: Deterministic Approaches, đã xuất bản tới lần thứ ba.
Từ ngày có lát cắt Tụy, nhiều người tiếp tục nghiên cứu nhiều cách chỉnh sửa để cho lát cắt này ngày càng đỡ tốn công đỡ tốn giờ hơn. Trong đó chính GS Hoàng Tụy cũng nhiều lần chỉnh sửa lát cắt của mình. Ta nói, đã tối ưu thì phải tối ưu cho trót.