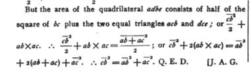Nếu nói chính xác thì không có tổng thống Mỹ nào có bài toán đăng báo chuyên ngành cả. Các đời tổng thống Mỹ có nhiều ngành nghề lắm, nghề luật sư và nghề nhà binh nhiều nhất, nhưng nghề toán chưa có ai.
Nhưng nếu dễ dãi hơn một chút, câu trả lời là có. Có một vị tổng thống có bài về toán đăng báo chuyên ngành, mà đăng trên báo chuyên ngành khác chứ không phải chuyên ngành toán.
Tôi muốn nói tới Tổng thống James A. Garfield (1831-1881). Ông làm tổng thống có 6 tháng rồi bị ám sát chết. Đường học vấn của ông không suôn sẻ. Lúc nhỏ, nhà nghèo, ông không được đi học nhiều, năm 17 tuổi mới vào trung học, 19 tuổi ra trường. Tự lực nuôi thân, ông vào đại học Western Reserve Eclectic Institute ở Ohio (nay đổi tên thành Hiram College) rồi chuyển đi Williams College ở Massachussetts, nơi ông tốt nghiệp cử nhân hạng Á khoa năm 26 tuổi.
Năm 1876, khi ông đã là dân biểu liên bang đại diện Ohio, tạp chí chuyên ngành sư phạm New-England Journal of Education tìm đến phỏng vấn ông. (New England là tên gọi vùng đông bắc Hoa Kỳ, trong đó có Massachussetts.) Chả biết mấy người nói chuyện gì với nhau mà đề tài chạy đến định lý Pytago (Pythagorean theorem).
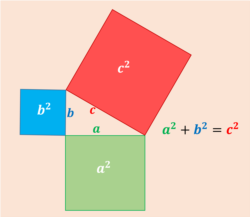
Chắc quý vị còn nhớ định lý này. Trong một tam giác vuông, hai cạnh bình phương cộng lại, bằng cạnh huyền bình phương. Vì bình phương là diện tích của hình vuông, nên định lý này thường được minh họa bằng hình vuông ghép bên ngoài tam giác.
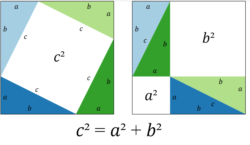
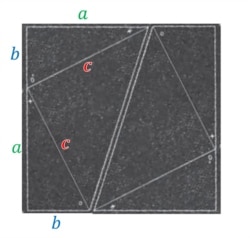
Trong các sách giáo khoa ngày nay, định lý Pytago được chứng minh bằng một hình đơn giản, bằng cách sắp xếp lại 4 hình tam giác và một hình vuông bên trong một hình vuông lớn hơn.
Nhưng vào thời trước, cách chứng minh tuy không khó nhưng nhiêu khê và liên quan các tỷ lệ rối ren. Tôi nghĩ là do ảnh hưởng của cách chứng minh nguyên thủy trong sách của Euclid thời Hy Lạp cổ đại.
Thế thì ông tổng thống tương lai James Garfield và tạp chí New-England Journal of Education nói chuyện gì không biết mà ông Garfield nêu lên định lý Pytago và bảo, tôi có cách chứng minh này hay lắm.
Và kết quả là New-England Journal of Education đăng lên báo. Nó đây. Trang 161, ngày 1 tháng 4, 1876.
Lời mở đầu của tạp chí có ghi là “chúng tôi chưa từng thấy” cách chứng minh này nên chia sẻ cho độc giả. Phía dưới có ký tắt J.A.G.
Cách chứng minh của Garfield là vẽ thêm một hình tam giác y hệt để tạo thành một hình thang. Diện tích của hình thang bao gồm 2 lần diện tích hình tam giác gốc, cộng với diện tích một miếng bằng nửa hình vuông cạnh “c”.
Diện tích hình thang bắt buộc phải bằng với (diện tích 2 tam giác gốc) + (diện tích hình vuông)/2
Diện tích hình thang bằng đáy cộng đáy, nhân cao, chia 2. Ở đây, hai đáy là a và b, cao là a + b, vậy diện tích hình thang bằng (a + b)(a + b)/2. Đó là vế bên trái.
Diện tích mỗi hình tam giác bằng (ab)/2. Hai hình tam giác là ab.
Diện tích hình nửa hình vuông còn lại, bằng c2/2.
Vậy vế bên phải gồm: ab + c2/2
Hai vế này bắt buộc phải bằng nhau.
(a + b)(a + b)/2 = ab + c2/2
Nhân ra, cộng trừ qua lại, sẽ ra định lý Pytago.
(a2 + 2ab + b2)/2 = ab + c2/2
a2 + b2 = c2
Đó là cách chứng minh của James A. Garfield. Vẫn còn hơi nhiều toán nhỉ? Có cách nào rút ngắn nguyên mảng toán ở trên không?
Có!
Garfield có sáng kiến vẽ thêm một hình tam giác nữa cho thành hình thang. Nếu mình tiếp tục sáng kiến của ông và vẽ thêm hình thang đó nữa, ghép vào, sẽ thành hình vuông.
Mà hình này chính là cách chứng minh thông dụng hiện nay: 4 tam giác và hình vuông c2 bên trong một hình vuông lớn hơn.
Riêng về định lý Pytago thì Garfield đúng là đi trước thời đại của ông nhiều.